What is Data Science and Does it Matter?
It starts like a typical data science job interview - I summarise my resume and they describe their core products. They describe what their data looks like and we have a very interesting chat about the structure of their data. But the interviewer keeps dancing around the topic of what my job will consist of and the whole thing become vaguer and vaguer until I'm forced to ask 'this sounds great but could you please explain what the job actually is?'
The answer is often some version of: 'Well, we're pretty sure we need a data scientist but could you explain what exactly a data scientist does?'
Nobody seems to know exactly what 'data science' is, let alone its almost synonym 'big data'. Maybe it's that most people are not accustomed to statisticians being interesting and it comes as a shock that statistics is useful to their business. Perhaps a new term just makes it easier to deal with.
Statistics has certainly become more valuable as the amount of data collected by businesses has exploded. We now collect so much data that we can create valuable products from the data itself, previously considered a mere by-product.
Is this really new? Reader's digest was doing data analysis on millions of households in the 70s (but they needed a mainframe to do it)[1]. They employed programmers and statisticians but no one we would recognize as a data scientist. Instead they had 300 people who together did what a data scientist can achieve today on a single MacBook Pro.
But the statistical element of data science and big data is often not new. I read a story in the New York Times about the problems in New York caused by restaurants pouring used cooking oil into sewers. Apparently the culprits were identified by 'big data'[2]:
They dug up data from the Business Integrity Commission, an obscure city agency that among other tasks certifies that all local restaurants have a carting service to haul away their grease. With a few quick calculations, comparing restaurants that did not have a carter with geo-spatial data on the sewers, the team was able to hand inspectors a list of statistically likely suspects.
Leaving aside the question of whether this is truly 'big data' - how different is this analysis from John Snow's analysis of Cholera cases in London in 1854? [3] [4]
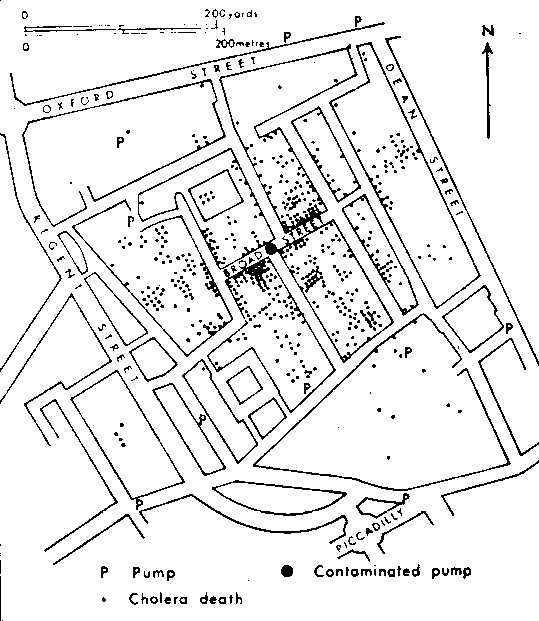
The statistical analysis is not different. The difference today is that the data was just sitting around in a database waiting to be discovered. This requires very different skills to traipsing around Victorian London looking for corpses.
It's now so easy to manipulate vast quantities of data that you don't need to employ a separate statistician, database guy and programmer. You hire someone who can code and do statistics too. This is the data scientist.
But this has lead to some confusion about what constitutes a data scientist. Very often data scientists are recruited by non-scientists, who aren't clear on what skills they should be hiring for. Hence the rise of the the hadoop engineer or SQL analyst hired as data scientist. Nothing wrong with these skills, but they don't make you a scientist.
Statistical know-how is essential. Large messy data sets with weird dependency structures and missing data will cause any data scientist pain and suffering. But at least those with statistical training know they are in trouble; and know what to do about it.
It's now time for data science as a profession to take stock and ask itself 'what is the core skill set?'. Or further than this, 'is data science a new statistical speciality or even a nascent field in its own right?'.
Come and join the debate at the Royal Statistical Society on the 11th of May